Vacuum state

Quantum field theory
(Feynman diagram)
History of...
Background Gauge theory Field theory Poincaré symmetry Quantum mechanics Spontaneous symmetry breaking
Symmetries Crossing Charge conjugation Parity Time reversal
Tools Anomaly Effective field theory Expectation value Faddeev–Popov ghosts Feynman diagram Lattice gauge theory LSZ reduction formula Partition function Propagator Quantization Renormalization Vacuum state Wick's theorem Wightman axioms
Equations Dirac equation Klein–Gordon equation Proca equations Wheeler–DeWitt equation
Standard Model Electroweak interaction Higgs mechanism Quantum chromodynamics Quantum electrodynamics Yang–Mills theory
Incomplete theories Quantum gravity String theory Supersymmetry Technicolor Theory of everything
Scientists Adler • Bethe • Bogoliubov • Callan • Candlin • Coleman • DeWitt • Dirac • Dyson • Fermi • Feynman • Fierz • Fröhlich • Gell-Mann • Goldstone • Gross • 't Hooft • Jackiw • Klein • Landau • Lee • Lehmann • Majorana • Nambu • Parisi • Polyakov • Salam • Schwinger • Skyrme • Stueckelberg • Symanzik • Tomonaga • Veltman • Weinberg • Weisskopf • Wilson • Witten • Yang • Yukawa • Hoodbhoy • Zimmermann • Zinn-Justin

In quantum field theory, the vacuum state (also called the vacuum) is the quantum state with the lowest possible energy. Generally, it contains no physical particles. Zero-point field is sometimes used as a synonym for the vacuum state of an individual quantized field.

According to present-day understanding of what is called the vacuum state or the quantum vacuum, it is "by no means a simple empty space",^[1] and again: "it is a mistake to think of any physical vacuum as some absolutely empty void."^[2] According to quantum mechanics, the vacuum state is not truly empty but instead contains fleeting electromagnetic waves and particles that pop into and out of existence.^[3]^[4]^[5]

The QCD vacuum of quantum chromodynamics is the object of study in the Large Hadron Collider and the Relativistic Heavy Ion Collider, and is related to the so-called vacuum structure of strong interactions.^[6]

1 Non-vanishing vacuum state
2 The energy of the vacuum state
3 The symmetry of the vacuum state
4 Electrical permittivity of vacuum state
5 Notations
6 Virtual particles
7 See also
8 References and notes
9 Further reading

Non-vanishing vacuum state

If the quantum field theory can be accurately described through perturbation theory, then the properties of the vacuum are analogous to the properties of the ground state of a quantum mechanical harmonic oscillator (or more accurately, the ground state of a QM problem). In this case the vacuum expectation value (VEV) of any field operator vanishes. For quantum field theories in which perturbation theory breaks down at low energies (for example, Quantum chromodynamics or the BCS theory of superconductivity) field operators may have non-vanishing vacuum expectation values called condensates. In the Standard Model, the non-zero vacuum expectation value of the Higgs field, arising from spontaneous symmetry breaking, is the mechanism by which the other fields in the theory acquire mass.

The energy of the vacuum state

Main article: Vacuum energy

In many situations, the vacuum state can be defined to have zero energy, although the actual situation is considerably more subtle. The vacuum state is associated with a zero-point energy, and this zero-point energy has measurable effects. In the laboratory, it may be detected as the Casimir effect. In physical cosmology, the energy of the cosmological vacuum appears as the cosmological constant. In fact, the energy of a cubic centimeter of empty space has been calculated figuratively to be one trillionth of an erg.^[7] An outstanding requirement imposed on a potential Theory of Everything is that the energy of the quantum vacuum state must explain the physically observed cosmological constant.

The symmetry of the vacuum state

For a relativistic field theory, the vacuum is Poincaré invariant. Poincaré invariance implies that only scalar combinations of field operators have non-vanishing VEV's. The VEV may break some of the internal symmetries of the Lagrangian of the field theory. In this case the vacuum has less symmetry than the theory allows, and one says that spontaneous symmetry breaking has occurred. See Higgs mechanism, standard model and Woit.^[8]

Electrical permittivity of vacuum state

In principle, quantum corrections to Maxwell's equations can cause the experimental electrical permittivity ε of the vacuum state to deviate from the defined scalar value ε₀ of the electric constant.^[9] These theoretical developments are described, for example, in Dittrich and Gies.^[5] In particular, the theory of quantum electrodynamics predicts that the vacuum should exhibit nonlinear effects that will make it behave like a birefringent material with ε slightly greater than ε₀ for extremely strong electric fields.^[10]^[11] Explanations for dichroism from particle physics, outside quantum electrodynamics, also have been proposed.^[12] Active attempts to measure such effects have been unsuccessful so far.^[13]

Notations

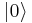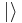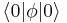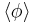The vacuum state is written as $|0\rangle$ or $|\rangle$ . The VEV of a field φ, which should be written as $\langle0|\phi|0\rangle$ , is usually condensed to $\langle\phi\rangle$ .

Virtual particles

The uncertainty principle in the form 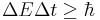$\Delta E\Delta t\ge\hbar$ implies that from the vacuum a particle pair with energy ΔE above the vacuum may undergo spontaneous creation for a short time Δt. These virtual particles are included in the definition of the vacuum.

References and notes

^ Astrid Lambrecht (Hartmut Figger, Dieter Meschede, Claus Zimmermann Eds.) (2002). Observing mechanical dissipation in the quantum vacuum: an experimental challenge; in Laser physics at the limits. Berlin/New York: Springer. p. 197. ISBN 3540424180. http://books.google.com/?id=0DUjDAPwcqoC&pg=PA197&dq=%22vacuum+state%22.
^ Christopher Ray (1991). Time, space and philosophy. London/New York: Routledge. Chapter 10, p. 205. ISBN 0415032210. http://books.google.com/?id=1F7xWULz0P0C&pg=RA1-PA205&dq=%22vacuum+state%22.
^ AIP Physics News Update,1996
^ Physical Review Focus Dec. 1998
^ ^a ^b Walter Dittrich & Gies H (2000). Probing the quantum vacuum: perturbative effective action approach. Berlin: Springer. ISBN 3540674284. http://books.google.com/?id=DyhyFSL7bNUC&pg=PP1&dq=intitle:Probing+intitle:the+intitle:Quantum+intitle:Vacuum.
^ Jean Letessier, Johann Rafelski (2002). Hadrons and Quark-Gluon Plasma. Cambridge University Press. p. 37 ff. ISBN 0521385369. http://books.google.com/?id=vSnFPyQaSTsC&pg=PR11&vq=Qgp+state&dq=weinberg+%22symmetry+%22.
^ Sean Carroll, Sr Research Associate - Physics, California Institute of Technology, June 22, 2006 C-SPAN broadcast of Cosmology at Yearly Kos Science Panel, Part 1
^ Peter Woit (2006). Not even wrong: the failure of string theory and the search for unity in physical law. New York: Basic Books. ISBN 0465092756. http://books.google.com/?id=pcJA3i0xKAUC&pg=PA93&dq=%22Higgs+field%22.
^ David Delphenich (2006). "Nonlinear Electrodynamics and QED". arXiv:hep-th/0610088 [hep-th].
^ Klein, James J. and B. P. Nigam, Birefringence of the vacuum, Physical Review vol. 135, p. B1279-B1280 (1964).
^ Mourou, G. A., T. Tajima, and S. V. Bulanov, Optics in the relativistic regime; § XI Nonlinear QED, Reviews of Modern Physics vol. 78 (no. 2), 309-371 (2006) pdf file.
^ Holger Gies; Joerg Jaeckel; Andreas Ringwald (2006). "Polarized Light Propagating in a Magnetic Field as a Probe of Millicharged Fermions". Physical Review Letters 97 (14). arXiv:hep-ph/0607118. Bibcode 2006PhRvL..97n0402G. doi:10.1103/PhysRevLett.97.140402.
^ Davis; Joseph Harris; Gammon; Smolyaninov; Kyuman Cho (2007). "Experimental Challenges Involved in Searches for Axion-Like Particles and Nonlinear Quantum Electrodynamic Effects by Sensitive Optical Techniques". arXiv:0704.0748 [hep-th].